[ 목차 ]
1. 힙정렬
2. 힙의 형태
3. 힙 구조
4. 힙의 배열 저장 방식
5. 노드의 높이
6. Max-Heapify
7. Max-Heampify의 수행시간
1. 힙정렬
1) 힙 구조의 특성을 이용한 정렬
2) 합병정렬과 동일한 수행시간
3) 삽입정렬과 동일한 제자리 정렬
4) 시간복잡도

2. 힙의 형태
1) 완전 이진 트리에 가까운 형태
2) 이진 트리 : 각 노드의 자식 수가 2개 이하인 경우
3) 완전 이진 트리 : root 노드부터 leaf 노드까지 빠짐없이 채워져 있는 트리
4) 완전 이진 트리는 왼쪽부터 채웠을 경우에만 해당

3. 힙 구조
1) 최대힙 특성 Max-Heap Property

1] 부모 노드의 값은 항상 자식 노드의 값보다 큼
2] 따라서 전체 트리의 root 노드 값이 가장 큼
3] 각 하위 트리 구조의 root 노드가 가장 큰 값을 지님
2) 최소힙 특성 Min-Heap Property

1] 자식 노드의 값은 항상 부모 노드의 값보다 큼
2] 따라서 전체 트리의 rott 노드 값이 가장 작음
3] 각 하위 트리 구조의 root 노드가 가장 작은 값을 지님
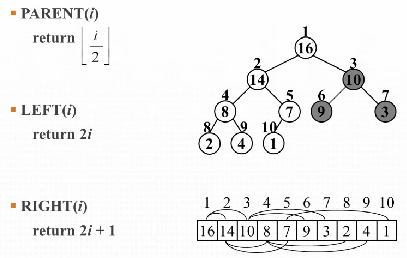
4. 힙의 배열 저장 방식
1) root 노드는 배열의 첫 번째 A[1]에 저장
2) 각가의 노드들은 레벨별로 저장

3] 힙을 배열에 저장하면 다음과 같이 검색이 가능
5. 노드의 높이
1) 현재 노드에서 leaf 노드까지 내려갈 때 가장 단순하게 내려가는 가장 긴 경로에서 거쳐야 하는 간선의 수
2) root 노드로부터 트리의 높이

3) heap은 완전 이진 트리 구조를 가지기 때문에 각 레벨마다 노드의 수가 2배씩 증가하기 때문
6. Max-Heapify
1) 배열이 주어졌을 때 배열이 Max-Heap이 되도록 만들어 주는 것
2) 노드가 입력으로 주어졌을 때 노드의 좌, 우, 하위 트리들은 max-heap 특성을 유지하지만 노드의 값이 하위 트리 값보다 작거나 같아서 max-heap 특성을 만족하지 않을 때 max-heap 특성이 되도록 바꾸는 연산
3) 주어진 노드값을 흘러내리게 해서 주어진 노드와 하위 트리가 max-heap 특성을 가질 수 있도록 변경

7. Max-Heampify의 수행시간

'T아카데미 > 컴퓨터 알고리즘 초급' 카테고리의 다른 글
| 8강. 퀵 정렬 (Quick Sort) (0) | 2020.04.13 |
|---|---|
| 7강. 힙정렬(Heap Sort)(2) (0) | 2020.04.12 |
| 5강. 합병정렬 (0) | 2020.04.09 |
| 4강. 삽입정렬 (0) | 2020.04.09 |
| 3강. 정렬문제 (0) | 2020.04.02 |



